Subdomein B1: Algoritmen
Een algoritme is een serie acties (of instructies) en beslissingen met een bepaald doel. De uitvoerder van deze instructies hoeft geen computer te zijn, maar kan ook een mens zijn. Zo zou je een partituur kunnen zien als algoritme voor een muziekstuk en een recept als een algoritme voor een gerecht. Beide worden uitgevoerd door een mens.
Basisbouwstenen voor algoritmen zijn opeenvolging, keuze en herhaling. Als een algoritme zichzelf aanroept, dan heet dat recursie.
Hieronder staat een voorbeeldalgoritme om te bepalen hoe vaak een bepaald woord in een gegeven tekst voorkomt.
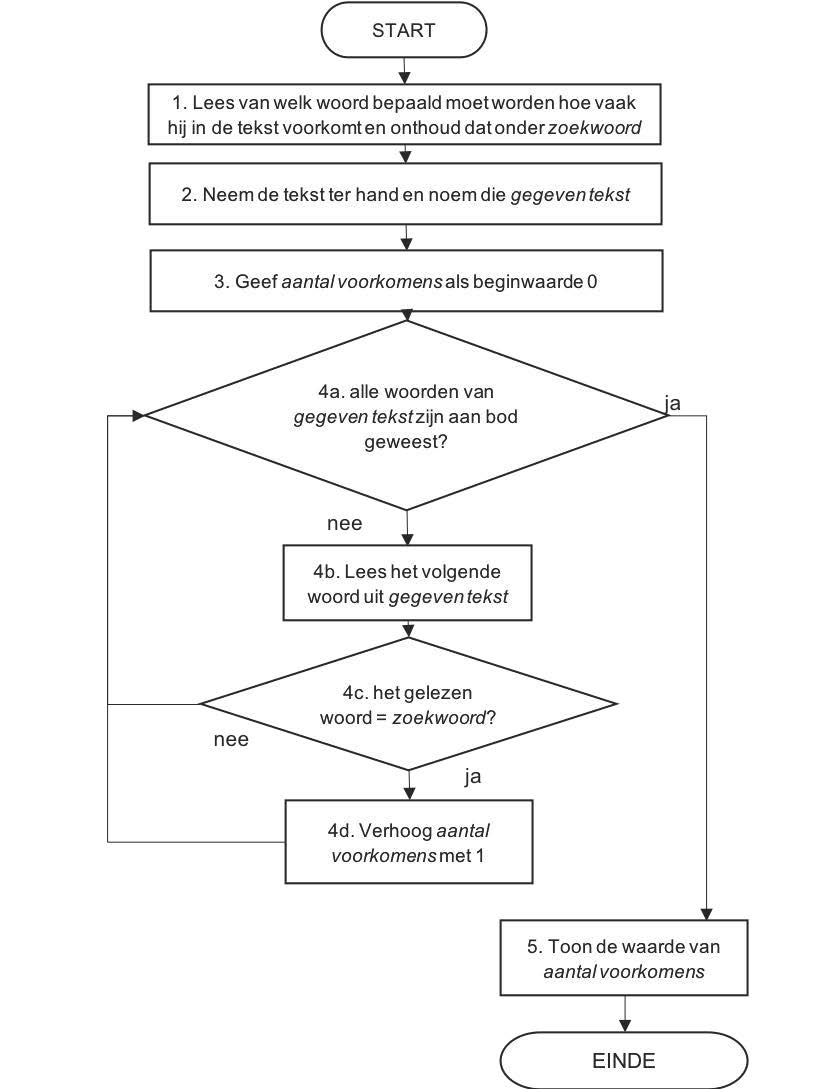
Over het voorbeeld:
- Het algoritme begint met een opeenvolging van instructies, stap 1, 2 en 3. Het algoritme doet hier altijd hetzelfde; onafhankelijk van de omstandigheden.
- Stap 4a tot en met 4d zijn onderdeel van een herhaling: zij worden meerdere malen uitgevoerd. Het aantal herhalingen hangt in dit voorbeeld af van het aantal woorden in de tekst, maar kan in het algemeen ook een van tevoren bepaald aantal zijn.
- Zowel stap 4a als 4c zijn keuzen: afhankelijk van de omstandigheden wordt gekozen welke volgende stap wordt doorlopen.
- Hetalgoritme is weergegeven als een flowchart, met instructies in blokken en pijlen tussen de blokken die de opeenvolging aangeven. In dit flowchart komen drie symbolen voor uit de norm ISO 5807:1985. Een algoritme kan ook in pseudocode worden weergegeven: herhalings- en keuzestructuren worden dan in woorden beschreven die doen denken aan een programmeertaal, bijvoorbeeld "ZOLANGvoorwaarde geldt, voer instructies uit.
Uit onderzoek (….) blijkt dat flowcharts didactische voordelen hebben. Bovendien is het in het geval van pseudocode nodig om afspraken te maken over de formulering van instructies, terwijl de blokken in de flowcharts teksten kunnen bevatten op een willekeurig niveau van abstractie (een concrete handeling of een complexere taak). Dit maakt flowcharts ruimer inzetbaar: zowel voor globaal ontwerp als voor weergave van gedetailleerde instructies. - In de flowchart worden enkele objecten aangeduid met een gekozen naam (gegeven tekst, aantal voorkomens). Zulke benoemde objecten in een algoritme zien we in een programma meestal terug als variabelen.
Correctheid
De correctheid van een algoritme kan op verschillende manieren aannemelijk worden gemaakt of zelfs bewezen. Dat laatste valt buiten het bereik van het examenprogramma. Testen is een veelgebruikte manier om de correctheid te onderzoeken (door fouten op te sporen), maar met testen is ongeschikt om de correctheid van een programma waterdicht aan te tonen.
Efficiëntie
Net als programma's kunnen algoritmen onderling vergeleken worden aan de hand van de (verwachte) rekentijd bij gegeven invoer. Meestal heeft een sneller ("efficiënter") algoritme de voorkeur. Een alternatief voor het hierboven beschreven algoritme is om de tekst eerst woord voor woord op te slaan om deze daarna pas te doorzoeken. Alle woorden worden dan twee keer gelezen en het algoritme is dus langer bezig. Dit nieuwe algoritme is nog steeds correct, maar minder efficiënt dan het voorbeeldalgoritme
De rekentijd kan in absolute zin worden beschouwd, maar interessanter is het om te kijken naar de rekentijd in relatie tot de grootte van de invoer, ook wel de complexiteit van een algoritme of programma genoemd. Welk effect heeft een verdubbeling van de invoer op de rekentijd, bijvoorbeeld? Hierop gaat het keuzethema G dieper in.