Een dynamisch model beschrijft het gedrag van een systeem in de tijd en wordt gekenmerkt door:1
- De begintoestand van het systeem;
- De factoren die van invloed zijn op de verandering van de toestand;
- De tijdstap waarin de verandering plaatsvindt;
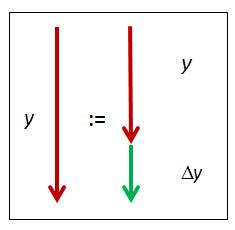
- De recursieve regel: nieuwe toestand := oude toestand + verandering.
In het experiment ter bepaling van de valversnelling geeft Tabel 1een beschrijving van de valbeweging opgedeeld in discrete tijdstappen Δt.
De toestandsvariabelen zijn de plaats y en de snelheidv; verandering wordt bepaald door de valversnelling g.
Uitgaande van de veronderstelling dat de valversnelling constant is, kan uit Tabel 1 een dynamisch model voor berekening van de valbeweging worden geconstrueerd. In dit model is de recursieve regel voor de berekening van de nieuwe toestand
Nieuwe plaats := oude plaats + verandering
v:= v + Δv
y:= y + Δy
De verandering van de snelheid per tijdstap wordt gegeven door de formule af te lezen uit Tabel 1:
Δv = g . Δt
De verandering van de plaats wordt evenzo gevonden als
Δy = v . Δt
geconstrueerd worden. Bij elke volgende tijdstap wordt de verandering van plaats en snelheid berekend en opgeteld bij de vorige toestand. De uitkomsten kunnen vergeleken worden met de gegevens van het experiment in Tabel 1.
| Hierboven vindt in feite de overgang plaats tussen het 'model van' de valbeweging (Tabel 1) naar een wiskundig 'model vóór' de valbeweging. Voor leerlingen is dit een grote conceptuele stap waaraan in de leersituatie expliciet aandacht gegeven moet worden. In lesmethoden is deze conceptuele stap vaak impliciet in de uitleg van het rekenmodel voor de beweging van een voorwerp.2 |
- K. Hooyman, Dynamische modellen vwo, Lesmodule voor wiskunde en NLT, SLO (2012)
- Overzicht dynamische modellen in de lesmethoden (pdf, 90 kB) Natuurkunde Overal, Newton, Nova, Pulsar, Stevin, Systematische natuurkunde.