Grafische modelregels
Aan de systeemdynamica1 is een grafische modelleertaal ontleend, waarmee verbanden tussen grootheden kunnen worden gemodelleerd.
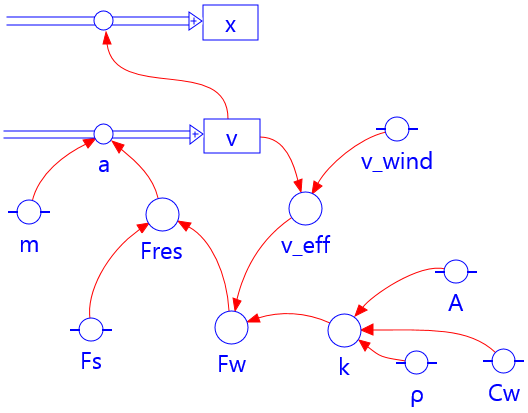
Fig 3.10 Grafisch model in Coach 7
In de grafisch weergave wordt een model opgebouwd uit een aantal vaste elementen. Hieronder worden deze elementen beschreven zoals het programma Coach2 die weergeeft:
- Toestandsvariabelen: de vakjes kunnen beschouwd worden als een bepaalde 'voorraad' of 'hoeveelheid' die kan toe- en afnemen, bijvoorbeeld, een hoeveelheid energie, een afstand tot een nulpunt of een aantal deeltjes (bij radioactief verval).
- Stroomvariabelen: deze variabelen geven aan hoeveel een 'voorraad' per tijdstap toe- of afneemt. In de bovengenoemde voorbeelden is dat dus hoeveel Joule, meter of deeltjes er in één tijdstap aan de voorraad worden toegevoegd of er juist af gaan.
- Hulp-variabelen: alle variabelen waarvan de verandering met een directe relatie kan worden weergegeven, worden aangegeven met een cirkeltje. Het kan bijvoorbeeld gaan om elektrisch vermogen (direct afhankelijk van stroomsterkte en spanning), de versnelling (afhankelijk van de resultante kracht en massa) en de activiteit van de bron (afhankelijk van het aantal deeltjes en de halveringstijd).
- Relatiepijlen: deze pijlen geven aan met behulp van welke andere toestands- of hulpvariabelen een bepaalde hulpvariabele of stroom berekend wordt.
- Constanten: een grootheid die in de looptijd van het model niet veranderd wordt aangegeven met een cirkel met twee uitsteeksels.
Het programma Coach genereert zelf de bijbehorende differentievergelijkingen op basis van het grafische model. Wel moeten de vergelijkingen voor de hulpvariabelen en stroomvariabelen handmatig worden ingevuld. Doordat het aantal bouwstenen beperkt is, wordt het voor leerlingen eenvoudiger om zelf een model samen te stellen. Ook is het eenvoudiger om in één oogopslag te zien hoe verschillende variabelen met elkaar samenhangen. De toestandsgrootheden en de veranderingsprocessen zijn duidelijk te herkennen en bij iedere grootheid is aangegeven waar deze van afhankelijk is.
Met deze bouwstenen kunnen leerlingen snel aan de slag en kunnen zij na een korte aanleertijd in sommige gevallen zelfs relatief geavanceerde modellen bouwen en interpreteren. Aan de andere kant blijkt ook dat een groep leerlingen de formele betekenis van de modelsymbolen niet doorziet, mede omdat de metafoor van voorraad-en-stromen een onvoldoende conceptuele basis biedt. Daarom is het belangrijk dat de relatie tussen de vergelijkingen en de bijbehorende grafische structuren in de beginfase duidelijk wordt gemaakt. 3, 4
1. J.W. Forrester, Learning through System Dynamics as Preparation for the 21st Century (1994)
2. CMA Science
3. E. Savelsbergh e.a., Modelleren en computermodellen in de β-vakken, Freudenthal Instituut (2008)
4. O. van Buuren, A. Heck, A.L. Ellermeijer, Understanding of Relation Structures of Graphical Models by Lower Secondary Students, Research in Science Education (2016)