Uitwerking
| Leselement | Uitvoering | Leeractiviteit |
|---|---|---|
| Uitwerken Modelregels opstellen en doorrekenen | Uitwerken van het model in wiskundige termen of grafische modelweergave Een beargumenteerde schatting maken voor parameterwaarden van het model op basis van gegevens Het model met een geschikte tijdstap doorrekenen |
klasleergesprek groepswerk |
De berekening van de valbeweging in opeenvolgende tijdstappen, zoals uitgewerkt in Tabel 2, kan gesystematiseerd worden in een iteratief rekenmodel.1
| Modelregels voor de valbeweging | |
|---|---|
| 1. Verandering snelheid | Δv=−g⋅Δt |
| 2. Nieuwe snelheid | v:=v+Δv |
| 3. Verandering plaats | Δy=v⋅Δt |
| 4. Nieuwe plaats | y:=y+Δy |
| 5. Nieuwe tijd | t:=t+Δt |
In de eerste twee modelregels wordt uit de versnelling een nieuwe snelheid berekend; vervolgens met deze snelheid een nieuwe plaats. De laatste modelregel zet de tijd metéén tijdstap vooruit voor een nieuwe berekening. Deze rekenstappen kunnen herhaald worden tot een gekozen eindsituatie is bereikt, bijvoorbeeld y = 0 . De verandering van een toestand van dit dynamische model kan dus geheel uitgedrukt worden in de valversnelling en de begintoestand van plaats en snelheid (of eindtoestand als teruggerekend wordt in de tijd).
Met de modelregels in Tabel 3 kan de valbeweging van een voorwerp waarop alleen de zwaartekracht werkt met de computer berekend worden. Daarvoor wordt meestal een specifieke modelleeromgeving gebruikt, zoals Coach2. Voor een eenvoudig verschijnsel als de valbeweging kunnen de berekeningen ook uitgevoerd worden in een spreadsheetprogramma zoals Excel3.
Noot:
De volgorde van de stappen in het rekenmodel is van belang.4 Eerst wordt de nieuwe snelheid berekend en dan de nieuwe plaats. Dit heeft te maken met het feit dat de snelheid niet constant is over een tijdsinterval Δt; bij een eenparig versnelde beweging neemt de snelheid lineair toe met de tijd. In feite zou gerekend moeten worden met de gemiddelde snelheid:
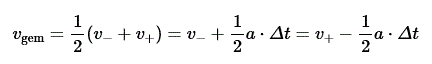
Daarin zijn v- en v+ de snelheden bij het begin, respectievelijk het einde, van een gegeven tijdstap.
In het rekenmodel in Tabel 3 is de benadering vgem≅v+ gekozen. In de numerieke wiskunde staat dit bekend als het Euler-Cromer algoritme. Dit algoritme verschilt van de gewone numerieke Eulermethode die werkt met de benadering vgem≅v− Dat wil zeggen de Eulermethode rekent met de beginsnelheid voor een gegeven tijdinterval en Euler-Cromer met de eindsnelheid. Beide methoden maken een fout van orde Δt over een eindig interval, maarde Euler-Cromer methode blijkt stabieler.5
Een nog betere benadering voor de numerieke iteratie van bewegingsvergelijkingen is de zogenaamde leapfrog methode, o.a. beschreven in de Feynman Lectures 6,die er in feite op neer komt dat de formule voor de gemiddelde snelheid hierboven numeriek wordt geïmplementeerd.7
1. Overzicht dynamische modellen in de lesmethoden NatuurkundeOveral, Newton, Nova, Pulsar, Stevin, Systematische natuurkunde. (pdf, 90 kB)
2. CMA-Science
3. D. Hoekzema, Mechanica & Modelleren, informatieboek VWO (2008)
4. H. van Bemmel en L. Koopman, Nova natuurkunde 4 vwo, Malmberg (2015)
5. T. Timberlake and J. Hasbun, Computation in Classical Physics, Am. J. Phys. (2008)
6. R.P. Feynman, The Feynman Lectures on Physics, vol. I, sec 9.6 (1962)
7. Ch.G. van Weert, De tweede wet van Newton en modelleren (pdf, 166 kB) (2013)