Harmonische potentiaal
In model symetrische put is de potentiele energie een rechte put. In veel situaties is het realistischer om te veronderstellen dat omringende atomen een quantumdeeltje binden in een harmonische potentiaalput alsof het deeltje een massa is aan een veer; zie model harmonische trilling. Voor dit geval kan de 1-dim Schrödingervergelijking analytisch worden opgelost.1 De discrete energiewaarden worden gevonden als
![]()
met ![]() de trillingsfrequentie van het massa-veersysteem. Uit de analytische oplossing volgt ook dat het systeem een karakteristieke debroglielengte
de trillingsfrequentie van het massa-veersysteem. Uit de analytische oplossing volgt ook dat het systeem een karakteristieke debroglielengte ![]() heeft.
heeft.
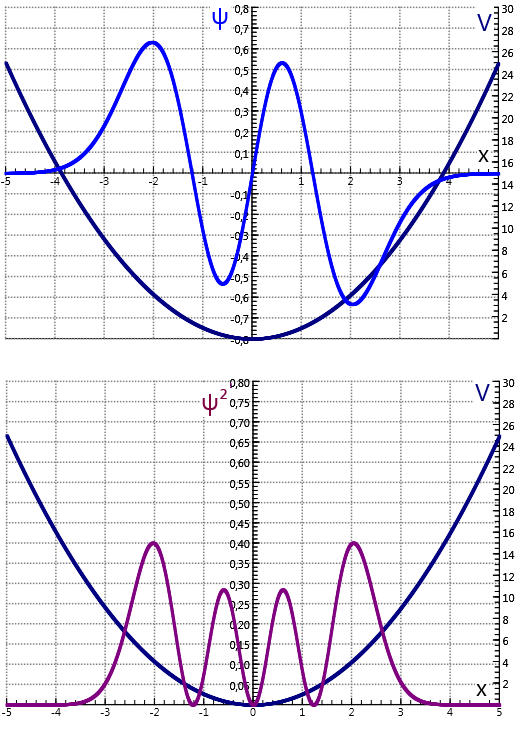
De modelregels6 worden vereenvoudigd door lengte en energie te schalenmet λ0 en E0. Door variatie van de variabele u kunnen de discrete energiewaarden numeriek gevonden worden. De voorwaarde is dat de golffuncties bij deze waarden eindig blijven en naar nul gaan ver van de oorsprong. De startwaarde in het voorbeeld hieronder correspondeert met toestand n=3.
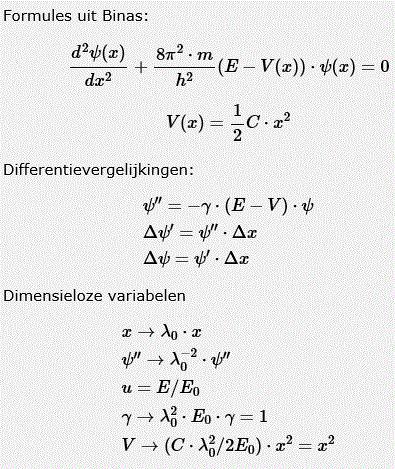
Modelregels
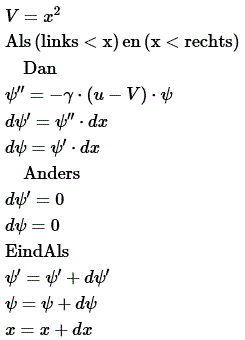
Download coachbestand met tekstuele model (cma7, 437 kB)
Grafisch model
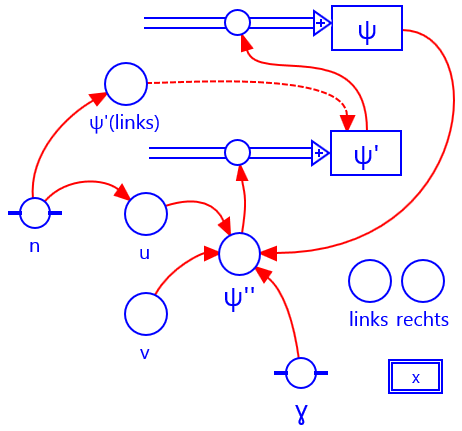
Download coachbestand met grafisch model (cma7, 451 kB)
Voorbeeld
Startwaarden
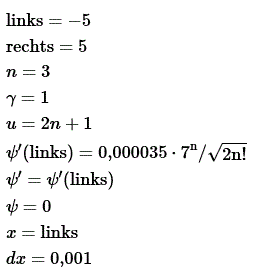
1. Wikipedia, Quantum harmonic oscillator
2. H. van Bemmel en L. Koopman, Nova natuurkunde 6 vwo, Malmberg (2015)